Facial Recognition with Collaborative Representation-Based Classification

The following post assumes some prior background in machine learning, such as familiarity with ordinary least squares (OLS).

Let’s talk about faces…

Collaborative representation-based classification is a neat way to implement ordinary least squares regression (which has continuous output) in order to classify new data points discretely. I am writing about this algorithm because it is elegant, but undertaught.¹ I explain the theory and implement the algorithm from scratch below.

We’ll use the YALE face database, consisting of 15 subjects in 11 slightly different poses, for a total of 165 64x64 pixel images, which I downloaded here ²³⁴⁵.

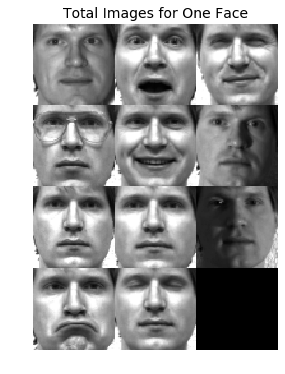
The data points \({x_0... x_n}\) are arranged in the columns of matrix \(X\) (size 4096x165) so that the first 11 columns correspond to the 11 images for the first face, the next 11 columns to the second face, and so on.

Theory

We begin by implementing ordinary least squares regression on \(X\), in which we find \(w\) to minimize the residual:

\[\begin{equation} w* = \arg\min_{w} \lVert \mathbf{Xw - x} \rVert_2^2 \end{equation}\]

We solve the normal equation to get \(\begin{equation} w* \end{equation}\):

\[\begin{equation} w* = (X^TX)^{-1}X^Tx \end{equation}\]

The first 11 elements of \(w\), which we will call \(w_0\), represent how much of each column of the first face we need to represent a new data point \(x\); the next 11 elements \(w_1\) represent how much of each column of the second face we need to represent \(x\); and so on.

Likewise, \(w_0\) corresponds to the first 11 columns of \(X\), which we will call \(X_0\).

To predict the face for each data point \(x\), we take the dot product \(\hat{y_i}\) of \(X_i\) and \(w_i\) for each face \(i\). We calculate the Euclidean distance between \(x\) and \(\hat{y_i}\). The face \(j\) out of \(i\) that yields the lowest distance will determine the label.

\[\begin{equation} j = \arg\min_{} \lVert \mathbf{x - \hat{y_i}} \rVert_2 \end{equation}\]

Code

The code for the algorithm is as follows:

def collab_rep(X_train, X_test, Y_train, Y_test):
    
    num_test_samples = X_test.shape[1]
    predicted_label = np.zeros((num_test_samples,))
    num_classifications = 15
    
    # OLS
    X = np.matrix(X_train)
    proj = np.linalg.pinv(np.dot(X.T,X)) * (X.T) 
    
    # for each new vector
    for i in range(0,num_test_samples):
        test_ex = np.matrix(X_test[:,i])
        p = proj * test_ex.T
        
        # compare the new vector to linear combinations of existing vectors by face
        dist = np.zeros((num_classifications,))
        num_in_training = int(X_train.shape[1] / num_classifications)
        for j in range(0,num_classifications):
            X_subset = X_train[:,j*num_in_training:(j+1)*num_in_training]
            w_subset = p[j*num_in_training:(j+1)*num_in_training]
            reconstructed = np.dot(X_subset, w_subset)
            dist[j] = np.linalg.norm(reconstructed - test_ex)
        
        # classify new vector according to minimum distance between the vector and reconstructed 
        predicted_label[i] = np.argmin(dist) + 1
        
    predicted_label = predicted_label.reshape(-1,1)
        
    # calculate the accuracy
    test_err = np.count_nonzero(predicted_label - Y_test)
    test_acc = 1-(test_err/100.0)
    
    return test_acc

We can run the code with 8 training and 3 test images per individual with 50 random splits to get a 96.62% accuracy.

Conclusion

In sum, the vectors of each face category “collaborate” via linear combinations in order to classify new faces (i.e., face category with the closest collaboration to the new face “wins”). We can further modify the algorithm to incorporate sparsity or lasso.

Compared to neural nets, collaborative representation-based classification is too inefficient to use practically. Nonetheless, it is an elegant discrete implementation of a continuous algorithm, with a high accuracy.

Full code on Github here.

References

1. You can read about collaborative representation-based classification in papers like this one. ↩

2. Deng Cai, Xiaofei He, Yuxiao Hu, Jiawei Han and Thomas Huang, “Learning a Spatially Smooth Subspace for Face Recognition”, CVPR’07. Bibtex source ↩

3. Deng Cai, Xiaofei He and Jiawei Han, “Spectral Regression for Efficient Regularized Subspace Learning”, ICCV’07. Bibtex source ↩

4. Deng Cai, Xiaofei He, Jiawei Han, and Hong-Jiang Zhang, “Orthogonal Laplacianfaces for Face Recognition”, IEEE TIP 2006. Bibtex source ↩

5. Xiaofei He, Shuicheng Yan, Yuxiao Hu, Partha Niyogi, and Hong-Jiang Zhang, “Face Recognition Using Laplacianfaces”, IEEE TPAMI 2005. Bibtex source ↩